机器学习：支持向量机（Support Vector Machine, SVM）

SVM是经典的监督型分类算法，广泛应用于机器学习、数据挖掘等领域。本质上SVM与线性回归方法类似，都是求一组权重系数。

感知机（perceptron）分类算法由于样本顺序和不同初值会导致解的多样性，解不唯一，亦不为最优，而SVM本质上是解最优目标方程的过程，解唯一，而且对于线性不可分的样本集会通过kernelling将样本映射到高维空间使其线性可分，再训练出分类边界，即超平面。因此SVM更具先进性。

一. 基本描述

如下图所示，SVM所解决的问题就是找出两组样本点间的一个最优分类边界，距离分类边界最近的那些点就是支持向量，在得到最终的分类边界时，支持向量到分类边界的距离也达到了最大。

png1

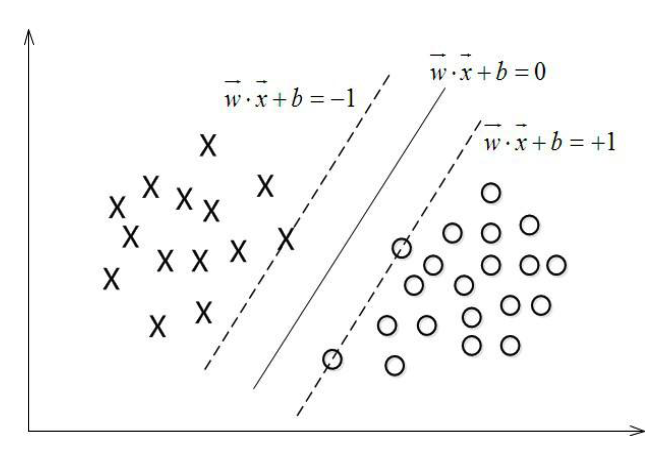
设超平面方程为：$w^T \dot{} x_i+b=0$；标签：$y_i=1~or~-1$，其中$i$为样本的index

根据向量和几何里面的一些知识我们可以轻松得到点$x_i$到超平面的距离为：

$\frac{w^T \dot{} x_i+b}{||w||}$

注意这里的距离是带有方向性的（可正可负），而标签的$y$值刚好可以抵消这种方向性，所以假设超平面的两侧分别为正负样本，没有错误的分类结果，那么点$x_i$到超平面的几何距离为：

$\frac{y_i(w^T \dot{} x_i+b)}{||w||}$

接下来要做的就是最大化这个几何距离，但是这个目标函数看起来有些复杂，不利于计算，我们要对其进行一定的简化。由图可以看出，对超平面起决定性作用的是虚线的上的那些点，也就是所谓的支持向量，我们知道，对超平面方程的所有系数（$w^T$和$b$）乘以相同的倍数并不会改变该超平面的位置，因此目标函数的分子，也就是$y_i(w^T \dot{} x_i+b)$可以取得任何值，我们不妨让其等于1，这种假设反映在几何平面上的意思就是，对于所有支持向量都满足$y_i(w^T \dot{} x_i+b)=1$，处支持向量之外的点满足$y_i(w^T \dot{} x_i+b)>1$，至此，我们可以将改最优化问题转换为：

$\max \frac{1}{||w||} ~~~s.t.~~y_i(w^T \dot{} x_i+b)\geqslant1, i=1,...,n$

二. 求解过程

最大化$\frac{1}{| |w| |}$ 可以转换为最小化$| |w| |^{2}$，因此最优化问题如下：

$\min \frac{1}{2}||w||^2 ~~~s.t.~~y_i(w^T \dot{} x_i+b)\geqslant1, i=1,...,n$

上述优化问题通过拉格朗日对偶性（通过求解与原问题等价的对偶问题得到原是问题的最优解，这样做的优点在于：一者对偶问题往往更加容易求解，二者可以自然的引入核函数用以解决非线性分类问题[1]）和KKT条件转换为另一个更利于快速解决的优化问题，该优化方程为：

$\max_{\alpha} \sum_{i} \alpha_{i}-\frac{1}{2}\sum_{i,j} \alpha_{i}\alpha_{j}y_iy_jx_i^Tx_j$ $s.t. ~~~ a_i\geqslant0,~\sum_{i}a_iy_i=0$

这里，$a_i$是拉格朗日算子，这个最优化问题通过SMO算法解决，是一种非常快速的二次规划优化算法。

三. 核函数

上面说的一切都是基于线性可分的情况，那么对于非线性情况改如何解决呢。我们可以想到的答案是将低维空间中的数据映射到高维空间使其线性可分，然后再进行分类。这样做理论上是可以的，但是维度过高会给计算带来很大的麻烦，产生维灾难。

解决方法是核函数，核函数可以达到将特征从低维转到高维的目的，但函数本身是在低维上进行计算的。

核函数的定义是计算两个向量在隐式映射过后的内积的函数，数据在原始空间的核函数的结果等于数据在特征空间的内积，即：

$K(x_1,x_2)=<\phi(x_1),\phi(x_2)>$

符号< >代表内积运算。

但是在实际求解中，我们并不是先定义$\phi(x)$，然后再进行内积运算得到核函数，原因上面已经提到过，特征空间维数可能会很高，计算比较困难，因此在实习求解中我们直接定义核函数$K(x_1,x_2)$，常用的核函数有以下几个：

（1）线性核

$K(x_1,x_2)=<x_1,x_2>$

原始空间的内积。

（2）多项式核

$K(x_1,x_2)=(<x_1,x_2>+R)^d$

代表的高维空间维度是$C_{m+d}^{d}$，其中$m$是原始空间的维度。

（3）高斯核

$K(x_1,x_2)=exp(-\frac{||x_1-x_2||^2}{2\sigma^2})$

高斯核可将空间映射到无穷维，$\sigma$过大会使得实际情况类似于一个低维子空间，而$\sigma$过小又会让任何数据都变得线性可分，这在一定程度上会影响分类的可信度，因此$\sigma$是一个关键的调控参数。

四. 松弛变量

我们知道实际的样本集中并不是每个数据都规规矩矩，有的数据是错误数据，有的是噪声，我们称之为outlier，这些数据会对最终的学习结果（超平面）造成不利的影响。为了解决此问题引入松弛变量$\xi_i$，令原有的约束条件变为：

$y_i(w^T \dot{} x_i+b)\geqslant 1-\xi_i, ~~i=1,...,n$

当然，我们需要对$\xi_i$进行约束，否则它的无限大可以认为所有点都是outlier，任意超平面都满足要求，最终的最优化问题如下：

$\max \frac{1}{2}||w||^2+C\sum_{i=1}^{n}\xi_i$ $s.t.~~y_i(w^T \dot{} x_i+b)\geqslant1-\xi_i, i=1,...,n$ $\xi_i \geqslant0, i=1,...,n$

其中C为超参数，是预设的一个常量，体验对异点的惩罚程度。

五. 多分类问题

我们知道SVM解决的是二分类问题，那么遇到多分类问题（假设共m类），我们可以将多分类问题转换为多个二分类问题：

（1）对每一类和其余类进行分类，这样得到m个分类器，哪个分类器概率高，就属于哪一类。

（2）两两做一次二分类，一共得到$C_m^2$个分类器，对于测试样本，经过$C_m^2$次分类，属于哪一类的结果出现次数最多，就将该类作为最终的结果。

六. 相关代码

机器学习实战里面有实现SVM的python代码，如下：

<span style="font-size:24px;">from numpy import * 
import random 

def loadDataSet(fileName):  #构建数据库和标记库
    dataMat = []; labelMat = [] 
    fr = open(fileName) 
    for line in fr.readlines(): 
        lineArr = line.strip().split('\t') 
        dataMat.append([float(lineArr[0]), float(lineArr[1])]) 
        labelMat.append(float(lineArr[2]))  #只有一列
    return dataMat, labelMat 


def selectJrand(i, m):  #生成一个随机数
    j=i 
    while(j==i): 
        j=int(random.uniform(0, m))  #生成一个[0, m]的随机数，int转换为整数。注意，需要import random
    return j 

def clipAlpha(aj, H, L):  #阈值函数
    if aj>H: 
        aj=H 
    if aj<L: 
        aj=L 
    return aj 

def smoSimple(dataMatIn, classLabels, C, toler, maxIter): 
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
    b = 0; m,n = shape(dataMatrix)
    alphas = mat(zeros((m,1)))
    iter = 0
    while(iter<maxIter):  #迭代次数
        alphaPairsChanged=0 
        for i in range(m):  #在数据集上遍历每一个alpha
            #print alphas 
            #print labelMat
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            #fXi=float(np.multiply(alphas, labelMat).T*dataMatrix*dataMatrix[i, :].T)+b  #.T也是转置
            Ei=fXi-float(labelMat[i]) 
            if((labelMat[i]*Ei<-toler) and (alphas[i]<C)) or ((labelMat[i]*Ei>toler) and (alphas[i]>0)): 
                j=selectJrand(i, m)  #从m中选择一个随机数，第2个alpha j
                fXj=float(multiply(alphas, labelMat).T*dataMatrix*dataMatrix[j, :].T)+b 
                Ej=fXj-float(labelMat[j]) 
                
                alphaIold=alphas[i].copy()  #复制下来，便于比较
                alphaJold=alphas[j].copy() 
                
                if(labelMat[i]!=labelMat[j]):  #开始计算L和H
                    L=max(0, alphas[j]-alphas[i]) 
                    H=min(C, C+alphas[j]-alphas[i]) 
                else: 
                    L=max(0, alphas[j]+alphas[i]-C) 
                    H=min(C, alphas[j]+alphas[i]) 
                if L==H: 
                    print 'L==H' 
                    continue 
                
                #eta是alphas[j]的最优修改量，如果eta为零，退出for当前循环
                eta=2.0*dataMatrix[i, :]*dataMatrix[j, :].T-\
                    dataMatrix[i, :]*dataMatrix[i, :].T-\
                    dataMatrix[j, :]*dataMatrix[j, :].T 
                if eta>=0: 
                    print 'eta>=0' 
                    continue 
                alphas[j]-=labelMat[j]*(Ei-Ej)/eta  #调整alphas[j] 
                alphas[j]=clipAlpha(alphas[j], H, L)  
                if(abs(alphas[j]-alphaJold)<0.00001):  #如果alphas[j]没有调整
                    print 'j not moving enough' 
                    continue 
                alphas[i]+=labelMat[j]*labelMat[i]*(alphaJold-alphas[j])  #调整alphas[i]
                b1=b-Ei-labelMat[i]*(alphas[i]-alphaIold)*\
                    dataMatrix[i, :]*dataMatrix[i, :].T-\
                    labelMat[j]*(alphas[j]-alphaJold)*\
                    dataMatrix[i, :]*dataMatrix[j, :].T 
                b2=b-Ej-labelMat[i]*(alphas[i]-alphaIold)*\
                    dataMatrix[i, :]*dataMatrix[j, :].T-\
                    labelMat[j]*(alphas[j]-alphaJold)*\
                    dataMatrix[j, :]*dataMatrix[j, :].T 
                
                if(0<alphas[i]) and (C>alphas[i]): 
                    b=b1 
                elif(0<alphas[j]) and (C>alphas[j]): 
                    b=b2 
                else: 
                    b=(b1+b2)/2.0 
                alphaPairsChanged+=1 
                
                print 'iter: %d i: %d, pairs changed %d' %(iter, i, alphaPairsChanged) 
        if(alphaPairsChanged==0): 
            iter+=1 
        else: 
            iter=0 
        print 'iteration number: %d' %iter
    return b, alphas 

                
if __name__=="__main__": 
    dataArr, labelArr=loadDataSet('testSet.txt') 
    b, alphas=smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
    
    print b, alphas </span>

七. 参考

1.支持向量机通俗导论（理解SVM的三层境界）

2.手把手教你实现SVM算法（一）

3.数据挖掘（机器学习）面试–SVM面试常考问题