深度学习：自编码器、神经网络基础

基本的自编码器（Autoencoder）是一个含有输入、隐含、输出的三层神经网络，它的目的是尽可能复现输入输出的关系。

一. 神经元

神经网络的最小组成单元是神经元，神经元的结构如下：

nnu

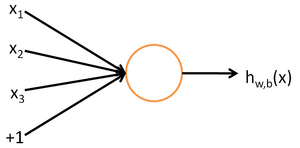
左边的$x_1,x_2,x_3$是运算输入值，$1$代表截距（为什么要有截距：我们知道线性拟合的时候如果不含常数项即截距，那么无论怎么拟合数据都必将经过原点，这很有可能和实际数据不符，在神经网络里也是这个原因）。

接着每个由输入到中间的那个圆圈的各条箭头线都附有权值$W$（长度等于输入个数+截距个数1）。

中间的圆圈代表激活函数$f(\cdot)$，通常有s激活函数（sigmoid，取值范围0~1）和双曲正切函数（tanh，取值范围-1~1）。

最后的$h(x)$代表输出：

$h_{W,b}(x)=f(W^Tx)=\sum_{i=1}^{3}W_ix_i+b$

二. 神经网络结构

最基本的神经网络由输入、隐含、输出三层结构组成，如下图：

nnu

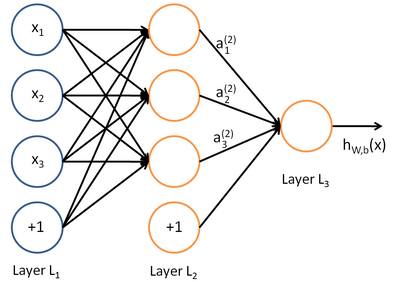
除了最后一层输出层，每一层的数据都包含额外的一项偏置结点，也就是之前说的截距。每一条带箭头的直线都代表一个权值（$h(x)$后的那条除外）。黄色的圈都代表对他的所有直接输入数据的加权和的激活处理。

从第一层开始向后一步一步进行加权和激活运算，这个过程叫做前向传播。合理的神经网络会尽可能拟合现有数据的输入输出关系，而要想达到这一目的，我们需要找到每一层网络上的合适的权重$W$，这一求解过程的方法就是反向传播算法。

三. 反向传播算法（Backpropagation，BP）

首先我们要设定一个代价函数来评价神经网络求解结果的好坏，和线性拟合的代价函数类似，都是二次损失。整体的代价函数如下：

$J(W,b)=\frac{1}{m}\sum_{i=1}^m(\frac{1}{2}\|\|h_{W,b}(x^{(i)})-y^{(i)}\|\|^2)+\frac{\lambda}{2}\sum_{l}\sum_{i}\sum_{j} (W_{ji}^{(l)})^2$

$m$是数据里有$m$个样例。

那么这里为什么要多一规则项（也称权重衰减项）$\frac{\lambda}{2}\sum_{l}\sum_{i}\sum_{j} (W_{ji}^{(l)})^2$呢：

因为我们为了稳定性要限制$W$的大小（一个稳定性解释的例子），必须添加一个关于的$W$的限制条件，也就是要使$\sum_{k=1}W_k^2\leqslant$某个常数。记得我们在本科时期学习的求解带有约束条件的目标函数的最优值吗？是的，那就是在原来的目标函数上添加约束条件的表达式。

$\lambda$是权重衰减参数，用于控制公式中两项的相对重要性。

我们的目标是针对参数$W$和$b$来求其函数$J(W,b)$的最小值。为了求解神经网络，我们需要将每一个参数$W^{(l)}_{ij}$和$b^{(l)}_i$初始化为一个很小的、接近零的随机值（比如说，使用正态分布${Normal}(0,\epsilon^2)$生成的随机值，其中$\epsilon$设置为0.01，之后对目标函数使用诸如批量梯度下降法的最优化算法。因为$J(W, b)$是一个非凸函数，梯度下降法很可能会收敛到局部最优解；但是在实际应用中，梯度下降法通常能得到令人满意的结果。

需要再次强调的是，要将参数进行随机初始化，而不是全部置为0。如果所有参数都用相同的值作为初始值，那么所有隐藏层单元最终会得到与输入值有关的、相同的函数。

梯度下降法的本质其实就是迭代求编导数：

$\begin{align} W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) \end{align}$

其中$\alpha$是学习速率。其中关键步骤是计算偏导数。反向传播算法是计算偏导数的一种有效方法，反向传播算法具体步骤如下：

（1）进行前馈传导计算，利用前向传导公式，得到$L_2, L_3, \ldots$直到输出层$L_{n_l}$的激活值

（2）对于第$n_l$层（输出层）的每个输出单元$i$，我们根据以下公式计算残差：

$\begin{align} \delta^{(n_l)}_i = \frac{\partial}{\partial z^{(n_l)}_i} \;\; \frac{1}{2} \left\|y - h_{W,b}(x)\right\|^2 = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i) \end{align}$

（3）对$l = n_l-1, n_l-2, n_l-3, \ldots, 2$的各个层，第$l$层的第$i$个节点的残差计算方法如下：

$\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i)$

以上逐次从后向前求导的过程即为“反向传导”的本意所在

（4）计算我们需要的偏导数，计算方法如下：

$\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)} \end{align}$

反向传播是批量梯度下降中的重要一步，上述公式的具体推导可以看这里。

现在给出批量梯度下降中的一次完整迭代：

（1）对于所有$l$，令 $\Delta W^{(l)} := 0$, $\Delta b^{(l)}:= 0$（设置为全零矩阵或全零向量，零元素为一个很小的、接近零的随机值）

（2）对于$i = 1$到$m$，

①使用反向传播算法计算 $\nabla_{W^{(l)}} J(W,b;x,y)$和$\nabla_{b^{(l)}} J(W,b;x,y)$

②计算 $\Delta W^{(l)} := \Delta W^{(l)} + \nabla_{W^{(l)}} J(W,b;x,y)$

③计算$\Delta b^{(l)} := \Delta b^{(l)} + \nabla_{b^{(l)}} J(W,b;x,y)$

（3）更新权重参数：

$\begin{align} W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\ b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align}$

现在，我们可以重复梯度下降法的迭代步骤来减小代价函数$J(W,b)$的值，进而求解我们的神经网络。求解结束以后就可以用来预测数据了。

四.稀疏自编码

所谓稀疏，就是让隐含层的部分神经元在多数时间处于抑制状态（sigmoid函数的抑制状态是0，tanh是-1）。稀疏的目的是为了发现数据中的一些结构，不做稀疏处理那么结构往往不具有代表性。事实上，这一简单的自编码神经网络通常可以学习出一个跟主元分析（PCA）结果非常相似的输入数据的低维表示。

接下来的部分解释来自知乎Charlotte的回答。稀疏自编码相对于多层BP神经网络只是在反向传播时多加了个稀疏项，就是你说的惩罚因子，这个惩罚因子就是KL散度值，也叫相对熵，可以理解为两个向量之间分布的差异，差异越小，相对熵越接近0。加这玩意儿不是为了“让隐层神经元个数始终不大于输入层神经元个数”，而是使隐含层的所有节点的输出和的均值接近稀疏性参数$\rho$，一个很接近0的值（前提是激活函数是sigmoid函数，如果激活函数是tanh函数，那这个$\rho$就接近于-1），简单的说，就是抑制大多数神经元的输出，这样就达到稀疏的目的了。其实隐含层的个数也是可以大于输入层的个数的，同样可以很好的学习。

加了惩罚因子后，总体代价函数可以表示为：

$\begin{align} J_{\rm sparse}(W,b) = J(W,b) + \beta \sum_{j=1}^{s_2} {\rm KL}(\rho || \hat\rho_j), \end{align}$ 其中$J(W,b)$如之前所定义，而$\beta$控制稀疏性惩罚因子的权重。 $\hat\rho_j$项则也（间接地）取决于$W,b$，因为它是隐藏神经元$j$的平均激活度，而隐藏层神经元的激活度取决于$W,b$。

为了对相对熵进行导数计算，我们可以使用一个易于实现的技巧，这只需要在你的程序中稍作改动即可。具体来说，前面在后向传播算法中计算第二层（$l=2$）更新的时候我们已经计算了

$\begin{align} \delta^{(2)}_i = \left( \sum_{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) f'(z^{(2)}_i), \end{align}$

现在我们将其换成

$\begin{align} \delta^{(2)}_i = \left( \left( \sum_{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) + \beta \left( - \frac{\rho}{\hat\rho_i} + \frac{1-\rho}{1-\hat\rho_i} \right) \right) f'(z^{(2)}_i) . \end{align}$

就可以了。

五.参考资料

UFLDL教程（有小练习）

知乎Charlotte的回答